3次元空間での円の中心の求め方
前回のコラムがくだけすぎでしたので、今回はまともなロジックを取り上げます。
平面上にある3点を通る円の中心位置は、どうやって求めるでしょうか。
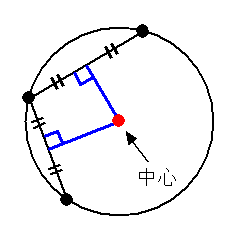
これについてはネット上でいくらでもロジックが解説されているので、簡単に結論だけを載せておきます。下図のように3点から2つの線分を作成し、その中点を通って線分と直交する直線の交点が円の中心になります。
平面上の円については容易なので問題ないとして、次に3次元空間にある円の中心位置と半径を求めるロジックを考えてみます。平面と同様に3点を指定すれば円が決まるので、3点の座標を $P_1(x_1,y_1,z_1), P_2(x_2,y_2,z_2), P_3(x_3,y_3,z_3)$ とします。
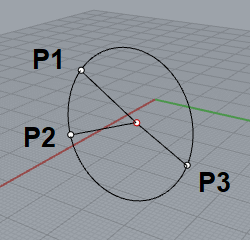
平面の例では2直線の交点を求めればよかったのですが、3次元空間では3平面の交点を求めることになります。空間内の平面は次の方程式で表されます。
$$
ax + by + cz + d = 0
$$
3点 $P_1, P_2, P_3$ を通る平面方程式の係数 $a \sim d$ は、各座標値を入力して連立方程式を解けば求まります。(未知数が4つで式が3つですが、$d$ を定数と置いて解くことができます)
次に、点 $P_1, P_2$ の中点を通り、3点を通る平面と垂直になる平面を考えます。中点の座標を $P_{12}$、また $X(x,y,z)$ とし、平面同士が垂直になるときは内積がゼロになるという性質を使用すると、平面の方程式は次式になります。
$$
(P_1-P_2) \cdot (X-P_{12}) = 0
$$
この式を展開すると、こうなります。
$$
(x_1-x_2) (x-x_{12}) + (y_1-y_2) (y-y_{12}) + (z_1-z_2) (z-z_{12}) = 0
$$
同様に、点 $P_2, P_3$ の中点を通り、3点を通る平面と垂直になる平面は次式になります。
$$
(P_2-P_3) \cdot (X-P_{23}) = 0
$$
これで3つの平面の方程式が得られたので、あとは連立させて解けば円の中心位置が求まり、それによって円の半径が計算できます。平面上にある円と比較すると計算が複雑になりますが、基本的なロジックは同じといえます。
試しに作成してみた VB.Net のコードを載せておきます。
Public Shared Sub Circle3D_Calculation(ByVal P_Ax As Single, ByVal P_Ay As Single, ByVal P_Az As Single,
ByVal P_Bx As Single, ByVal P_By As Single, ByVal P_Bz As Single,
ByVal P_Cx As Single, ByVal P_Cy As Single, ByVal P_Cz As Single,
ByRef Center_x As Single, ByRef Center_y As Single,
ByRef Center_z As Single, ByRef Circle_R As Single)
'-------------------------------------------------------------
' 空間上の3点から、その点を通る円の中心位置と半径を求める
'
' P_Ax, P_Ay, P_Az : 1点目の座標
' P_Bx, P_By, P_Bz : 2点目の座標
' P_Cx, P_Cy, P_Cz : 3点目の座標
'
' Center_x, Center_y, Center_z : 円の中心の座標
' Circle_R : 円の半径
'-------------------------------------------------------------
Dim Coef_A As Single, Coef_B As Single, Coef_C As Single, Coef_D As Single
Dim P_ABx As Single = (P_Ax + P_Bx) / 2
Dim P_ABy As Single = (P_Ay + P_By) / 2
Dim P_ABz As Single = (P_Az + P_Bz) / 2
Dim P_BCx As Single = (P_Bx + P_Cx) / 2
Dim P_BCy As Single = (P_By + P_Cy) / 2
Dim P_BCz As Single = (P_Bz + P_Cz) / 2
Call Solve_PlaneEquation(P_Ax, P_Ay, P_Az, P_Bx, P_By, P_Bz, P_Cx, P_Cy, P_Cz,
Coef_A, Coef_B, Coef_C, Coef_D)
Dim C_a1 As Single = Coef_A
Dim C_b1 As Single = Coef_B
Dim C_c1 As Single = Coef_C
Dim C_d1 As Single = Coef_D
Dim C_a2 As Single = P_Ax - P_Bx
Dim C_b2 As Single = P_Ay - P_By
Dim C_c2 As Single = P_Az - P_Bz
Dim C_d2 As Single = -(P_Ax - P_Bx) * P_ABx - (P_Ay - P_By) * P_ABy - (P_Az - P_Bz) * P_ABz
Dim C_a3 As Single = P_Bx - P_Cx
Dim C_b3 As Single = P_By - P_Cy
Dim C_c3 As Single = P_Bz - P_Cz
Dim C_d3 As Single = -(P_Bx - P_Cx) * P_BCx - (P_By - P_Cy) * P_BCy - (P_Bz - P_Cz) * P_BCz
Call Solve_3unkLinerEquation(C_a1, C_b1, C_c1, C_d1, C_a2, C_b2, C_c2, C_d2,
C_a3, C_b3, C_c3, C_d3, Center_x, Center_y, Center_z)
Dim Circle_R0 As Single = (P_Ax - Center_x) ^ 2 + (P_Ay - Center_y) ^ 2 + (P_Az - Center_z) ^ 2
Dim Circle_R1 As Single = (P_Bx - Center_x) ^ 2 + (P_By - Center_y) ^ 2 + (P_Bz - Center_z) ^ 2
Dim Circle_R2 As Single = (P_Cx - Center_x) ^ 2 + (P_Cy - Center_y) ^ 2 + (P_Cz - Center_z) ^ 2
Circle_R = Math.Sqrt((Circle_R0 + Circle_R1 + Circle_R2) / 3)
End Sub
Public Shared Sub Solve_PlaneEquation(ByVal P_Ax As Single, ByVal P_Ay As Single, ByVal P_Az As Single,
ByVal P_Bx As Single, ByVal P_By As Single, ByVal P_Bz As Single,
ByVal P_Cx As Single, ByVal P_Cy As Single, ByVal P_Cz As Single,
ByRef Coef_A As Single, ByRef Coef_B As Single,
ByRef Coef_C As Single, ByRef Coef_D As Single)
'----------------------
' 平面方程式の係数
'----------------------
Coef_A = (P_By - P_Ay) * (P_Cz - P_Az) - (P_Cy - P_Ay) * (P_Bz - P_Az)
Coef_B = (P_Bz - P_Az) * (P_Cx - P_Ax) - (P_Cz - P_Az) * (P_Bx - P_Ax)
Coef_C = (P_Bx - P_Ax) * (P_Cy - P_Ay) - (P_Cx - P_Ax) * (P_By - P_Ay)
Coef_D = -(Coef_A * P_Ax + Coef_B * P_Ay + Coef_C * P_Az)
End Sub
Public Shared Sub Solve_3unkLinerEquation(ByVal C_a1 As Single, ByVal C_b1 As Single,
ByVal C_c1 As Single, ByVal C_d1 As Single,
ByVal C_a2 As Single, ByVal C_b2 As Single,
ByVal C_c2 As Single, ByVal C_d2 As Single,
ByVal C_a3 As Single, ByVal C_b3 As Single,
ByVal C_c3 As Single, ByVal C_d3 As Single,
ByRef Res_x As Single, ByRef Res_y As Single,
ByRef Res_z As Single)
'----------------------------
' 3元1次連立方程式を解く
'----------------------------
Dim C_1 As Single = C_a1 * C_c2 - C_a2 * C_c1
Dim C_2 As Single = C_b1 * C_c2 - C_b2 * C_c1
Dim C_3 As Single = C_c2 * C_d1 - C_c1 * C_d2
Dim C_4 As Single = C_a2 * C_c3 - C_a3 * C_c2
Dim C_5 As Single = C_b2 * C_c3 - C_b3 * C_c2
Dim C_6 As Single = C_c3 * C_d2 - C_c2 * C_d3
Res_x = -(C_3 * C_5 - C_6 * C_2) / (C_1 * C_5 - C_4 * C_2)
Res_y = -(C_1 * Res_x + C_3) / C_2
Res_z = -(C_a1 * Res_x + C_b1 * Res_y + C_d1) / C_c1
End Sub
なお、当然ながら3点が直線上にあったり、点の位置が重なっていたりしたら円は求まりません。その場合は上のコードではエラーが発生するので、入力データについてはユーザー自身で確認しておいてください。
では、次回は球の中心位置を求めるロジックについて記載する予定です。