球の中心の求め方
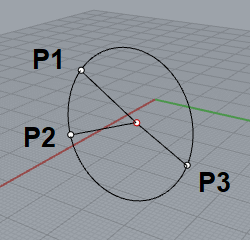
前回のコラムで3次元空間での円の中心の求め方について記述したので、次に空間内にある球の中心を求めるロジックについて考えてみます。球については、表面上にある4点の座標が指定されたら形状が確定します。(3点の座標と半径が指定されても球の形状は求まりますが、ここでは半径が未知の場合を対象とします)
球の中心の座標を $x_0, y_0, z_0$、半径を $r$ とすると、球の方程式は次式となります。
$$
(x – x_0)^2 + (y – y_0)^2 + (z – z_0)^2 = r^2
$$
球の表面上にある4点の座標値を $(x_1,y_1,z_1) \sim (x_4,y_4,z_4)$ とすると、以下の連立方程式を解けば中心位置と半径が求まります。
$$
\begin{eqnarray}
(x_1\, – x_0)^2 + (y_1\, – y_0)^2 + (z_1\, – z_0)^2 &=& r^2 \\
(x_2\, – x_0)^2 + (y_2\, – y_0)^2 + (z_2\, – z_0)^2 &=& r^2 \\
(x_3\, – x_0)^2 + (y_3\, – y_0)^2 + (z_3\, – z_0)^2 &=& r^2 \\
(x_4\, – x_0)^2 + (y_4\, – y_0)^2 + (z_4\, – z_0)^2 &=& r^2
\end{eqnarray}
$$
未知数が4つで式が4つなので、確かに解くことはできます。しかしながら、4元2次連立方程式なので、これを展開していくとものすごく長い式になってしまいます。十分な気合があればやってみてもいいと思いますが、ここではもっと容易でプログラミングに適した方法がないか考えてみます。
4点のうち3点を通る円は、球の切断面になります。
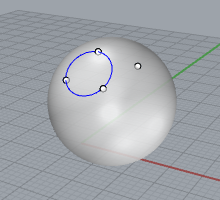
したがって、この円の中心を通る法線上のどこかに球の中心があることになります。
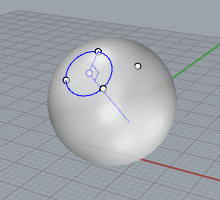
ここまで書けばわかると思いますが、4点から円を2つ作り、それぞれの中心を通る法線の交点が球の中心になります。

このロジックを使えば、プログラミングは比較的容易です。試しに VB.Net で作成したコードを載せておきます。
Public Shared Sub Sphere_Calculation(ByVal P_Ax As Single, ByVal P_Ay As Single, ByVal P_Az As Single,
ByVal P_Bx As Single, ByVal P_By As Single, ByVal P_Bz As Single,
ByVal P_Cx As Single, ByVal P_Cy As Single, ByVal P_Cz As Single,
ByVal P_Dx As Single, ByVal P_Dy As Single, ByVal P_Dz As Single,
ByRef Center_x As Single, ByRef Center_y As Single,
ByRef Center_z As Single, ByRef Circle_R As Single)
'-------------------------------------------------------------
' 空間上の4点から、その点を通る球の中心位置と半径を求める
'
' P_Ax, P_Ay, P_Az : 1点目の座標
' P_Bx, P_By, P_Bz : 2点目の座標
' P_Cx, P_Cy, P_Cz : 3点目の座標
' P_Dx, P_Dy, P_Dz : 4点目の座標
'
' Center_x, Center_y, Center_z : 円の中心の座標
' Circle_R : 円の半径
'-------------------------------------------------------------
Dim Center_x2d(1) As Single, Center_y2d(1) As Single, Center_z2d(1) As Single
Dim Circle_R2d(1) As Single
Dim Tri_NX(1) As Single, Tri_NY(1) As Single, Tri_NZ(1) As Single
Dim Center_x3d(1) As Single, Center_y3d(1) As Single, Center_z3d(1) As Single
Dim Closest_Dist As Single, ErrNo As Integer
'点A,B,Cを通る円の中心
Call Circle3D_Calculation(P_Ax, P_Ay, P_Az, P_Bx, P_By, P_Bz, P_Cx, P_Cy, P_Cz,
Center_x2d(0), Center_y2d(0), Center_z2d(0), Circle_R2d(0))
'点A,B,Cを通る平面の法線ベクトル
Call Tri_NormalVector(P_Ax, P_Ay, P_Az, P_Bx, P_By, P_Bz, P_Cx, P_Cy, P_Cz,
Tri_NX(0), Tri_NY(0), Tri_NZ(0))
'点A,B,Dを通る円の中心
Call Circle3D_Calculation(P_Ax, P_Ay, P_Az, P_Bx, P_By, P_Bz, P_Dx, P_Dy, P_Dz,
Center_x2d(1), Center_y2d(1), Center_z2d(1), Circle_R2d(1))
'点A,B,Dを通る平面の法線ベクトル
Call Tri_NormalVector(P_Ax, P_Ay, P_Az, P_Bx, P_By, P_Bz, P_Dx, P_Dy, P_Dz,
Tri_NX(1), Tri_NY(1), Tri_NZ(1))
'2直線の最接近位置
Call Line_ClosestPoint(Center_x2d(0), Center_y2d(0), Center_z2d(0),
Center_x2d(0) + Tri_NX(0), Center_y2d(0) + Tri_NY(0), Center_z2d(0) + Tri_NZ(0),
Center_x2d(1), Center_y2d(1), Center_z2d(1),
Center_x2d(1) + Tri_NX(1), Center_y2d(1) + Tri_NY(1), Center_z2d(1) + Tri_NZ(1),
Center_x3d(0), Center_y3d(0), Center_z3d(0),
Center_x3d(1), Center_y3d(1), Center_z3d(1),
Closest_Dist, ErrNo)
'最接近位置間の中点を球の中心とする
Center_x = (Center_x3d(0) + Center_x3d(1)) / 2
Center_y = (Center_y3d(0) + Center_y3d(1)) / 2
Center_z = (Center_z3d(0) + Center_z3d(1)) / 2
Dim Circle_R0 As Single = (P_Ax - Center_x) ^ 2 + (P_Ay - Center_y) ^ 2 + (P_Az - Center_z) ^ 2
Dim Circle_R1 As Single = (P_Bx - Center_x) ^ 2 + (P_By - Center_y) ^ 2 + (P_Bz - Center_z) ^ 2
Dim Circle_R2 As Single = (P_Cx - Center_x) ^ 2 + (P_Cy - Center_y) ^ 2 + (P_Cz - Center_z) ^ 2
Dim Circle_R3 As Single = (P_Dx - Center_x) ^ 2 + (P_Dy - Center_y) ^ 2 + (P_Dz - Center_z) ^ 2
Circle_R = Math.Sqrt((Circle_R0 + Circle_R1 + Circle_R2 + Circle_R3) / 4)
End Sub
Shared Sub Tri_NormalVector(ByVal Tri_X1 As Single, ByVal Tri_Y1 As Single, ByVal Tri_Z1 As Single,
ByVal Tri_X2 As Single, ByVal Tri_Y2 As Single, ByVal Tri_Z2 As Single,
ByVal Tri_X3 As Single, ByVal Tri_Y3 As Single, ByVal Tri_Z3 As Single,
ByRef Tri_NX As Single, ByRef Tri_NY As Single, ByRef Tri_NZ As Single)
'-----------------------------------------------------------
' 三角形サーフェスの法線ベクトルの計算
'
' Tri_X1, Tri_Y1, Tri_Z1 : 三角形の頂点の座標(1点目)
' Tri_X2, Tri_Y2, Tri_Z2 : 三角形の頂点の座標(2点目)
' Tri_X3, Tri_Y3, Tri_Z3 : 三角形の頂点の座標(3点目)
'
' Tri_NX, Tri_NY, Tri_NZ : 法線ベクトルの X,Y,Z 成分
'-----------------------------------------------------------
Dim Tri_NXYZ As Single
Tri_NX = Tri_Y1 * (Tri_Z2 - Tri_Z3) + Tri_Y2 * (Tri_Z3 - Tri_Z1) + Tri_Y3 * (Tri_Z1 - Tri_Z2)
Tri_NY = Tri_Z1 * (Tri_X2 - Tri_X3) + Tri_Z2 * (Tri_X3 - Tri_X1) + Tri_Z3 * (Tri_X1 - Tri_X2)
Tri_NZ = Tri_X1 * (Tri_Y2 - Tri_Y3) + Tri_X2 * (Tri_Y3 - Tri_Y1) + Tri_X3 * (Tri_Y1 - Tri_Y2)
Tri_NXYZ = Math.Sqrt(Tri_NX ^ 2 + Tri_NY ^ 2 + Tri_NZ ^ 2)
If Tri_NXYZ > 0 Then
Tri_NX /= Tri_NXYZ
Tri_NY /= Tri_NXYZ
Tri_NZ /= Tri_NXYZ
Else
Tri_NX = 0
Tri_NY = 0
Tri_NZ = 0
End If
End Sub
上記コードで使用しているサブルーチンについては、3次元空間での円の中心の求め方 と 3次元空間での2直線の最接近位置 を参照してください。
また、当然ながら4点が同一平面上にあったり、点の位置が重なっていたりしたら球は求まりません。その場合は上のコードではエラーが発生するので、入力データについてはユーザー自身で確認しておいてください。
連立方程式を力業で解かなくても、3D モデルを見ているうちにプログラミング化に適した方法を思いつくことがあります。その際、今までに作成したサブルーチンを流用できることが多くあるので、プログラムはできるだけ標準化した仕様で作成しておくことをお勧めします。