最小二乗法による2次元データの曲面近似
計測データ等を近似する場合、最小二乗法による曲線近似が使われることが多くあります。例えば、以下のデータを1次~5次曲線で近似するとこういう感じです。
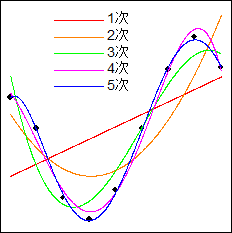
最小二乗法による曲線近似についてはネット上に多くの情報があるので、検索すればいくらでもコードは見つかるはずです。私は学生時代に Fortran でプログラムを作成し、それを VB.Net と C# にコンバートして今でも使っています。もちろん、プログラムを作らなくても Excel で近似曲線を作成することもできます。
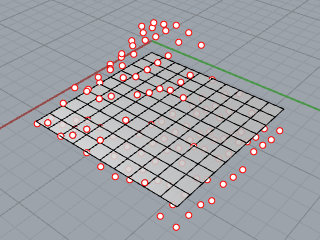
曲線近似についてはここで紹介するまでもありませんが、では下図のように2次元に分布したデータを最小二乗法で近似する場合はどうしたらいいでしょうか。

この場合は2変数 $ x,y $ による分布なので曲線ではなく曲面での近似になりますが、このようなケースはあまり需要がないのか、ネット上でも情報は少ないようです。以前、このような曲面近似を行ったことがあるので、ロジックについて説明してみます。
この場合の近似式は以下の通りとなります。
$$
\begin{eqnarray}
z &=& a_{00} + a_{10} \, x + a_{11} \, x\, y + a_{01} \, y \\
& & +a_{20} \, x^2 + a_{21} \, x^2 \, y + a_{22} \, x^2 \, y^2 + a_{12} \, x \, y^2 + a_{02} \, y^2 + … \\
&=& \sum_{n=0}^{N} \sum_{m=0}^{M} a_{nm} \, x^n \, y^m
\end{eqnarray}
$$
$ i $ 番目の点 $ (x_i,y_i) $ でのデータを $ m_i $ とすると、データと近似値との誤差 $ \epsilon_i $ と誤差の二乗和 $ E $ は次式となります。
$$
\begin{eqnarray}
\epsilon_i &=& z (x_i, y_i) – m_i \\
& & \\
E &=& \sum (\epsilon_i^2)
\end{eqnarray}
$$
したがって、誤差の二乗和 $ E $ を最小にするような係数 $ a_{00} \sim a_{NM} $ を求めればいいことになります。 $ E $ が最小になるときは各係数に対して勾配がゼロになることから、偏微分してゼロという性質を利用します。
$$
\begin{eqnarray}
\frac{\partial E}{\partial a_{nm}} &=& \frac{\partial}{\partial a_{nm}} \sum (\epsilon_i^2) \\
&=& \sum \frac{\partial \epsilon_i^2}{\partial a_{nm}} \\
&=& 2 \sum \epsilon_i \left( \frac{\partial \epsilon_i}{\partial a_{nm}} \right) \\
&=& 2 \sum \left\{ \left( z (x_i,y_i) – m_i \right) \frac{\partial z (x_i,y_i)}{\partial a_{nm}} \right\} \\
&=& 0
\end{eqnarray}
$$
ここで、
$$
\begin{eqnarray}
\frac{\partial z (x_i,y_i)}{\partial a_{nm}} = x_i^n \, y_i^m
\end{eqnarray}
$$
なので、
$$
\begin{eqnarray}
\sum \left\{ \left( z (x_i,y_i) – m_i \right) \, x_i^n \, y_i^m \right\} &=& 0 \ \ \ (n=0 \sim N, m=0 \sim M)\\
\sum \left\{ \left( \sum_{n=0}^{N} \sum_{m=0}^{M} a_{nm} \, x_i^n \, y_i^m – m_i \right) \, x_i^n \, y_i^m \right\} &=& 0 \\
\sum \left\{ \left( \sum_{n=0}^{N} \sum_{m=0}^{M} a_{nm} \, x_i^n \, y_i^m \right) \, x_i^n \, y_i^m \right\} &=& \sum \left( m_i \, x_i^n \, y_i^m \right)
\end{eqnarray}
$$
上式は $(n+1)(m+1)$ 元1次連立方程式となり、これを解くことで係数 $a_{nm}$ が求まります。ただし、条件としてデータ $ m_i $ の個数が $(n+1)(m+1)$ 個以上である必要があります。
例えば $ N=1, M=1 $ のときは以下の連立方程式になります。
$$
\begin{eqnarray}
a_{00} \sum 1 + a_{10} \sum x_i + a_{01} \sum y_i + a_{11} \sum x_i \, y_i &=& \sum m_i \\
a_{00} \sum x_i + a_{10} \sum x_i^2 + a_{01} \sum x_i \, y_i + a_{11} \sum x_i^2 \, y_i &=& \sum m_i \, x_i \\
a_{00} \sum y_i + a_{10} \sum x_i \, y_i + a_{01} \sum y_i^2 + a_{11} \sum x_i \, y_i^2 &=& \sum m_i \, y_i \\
a_{00} \sum x_i \, y_i + a_{10} \sum x_i^2 \, y_i + a_{01} \sum x_i \, y_i^2 + a_{11} \sum x_i^2 \, y_i^2 &=& \sum m_i \, x_i \, y_i
\end{eqnarray}
$$
この場合、データ数が4個以上であれば行列の計算を用いて係数 $ a_{00},a_{10},a_{01},a_{11} $ が求まります。
上の図で示したデータについて、曲面近似を行ってみました。$ N=M=0 $ の場合、下図のようにデータ平均値の平面になります。
続いて $ N=M=1 $ の近似曲面。

$ N=M=2 $ の近似曲面。

$ N=M=3 $ の近似曲面。

$ N=M=4 $ の近似曲面。

$ N=M=5 $ の近似曲面。

$ N=M=6 $ の近似曲面。

次数を上げていけばいくらでも近似できますが、そうすると外れ値に引っ張られて曲面が波打つことになります。最適な次数を求めるためには、一般的には「赤池情報量規準(AIC)」というものを使います。
AIC についてはネット上にいくらでも情報があるので、説明は省略して各次数での AIC を計算すると下のグラフの通りになります。
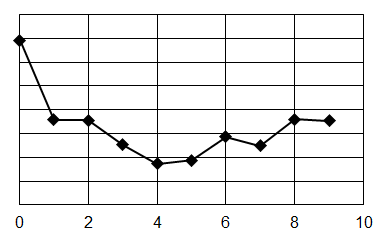
この例では AIC が最小になるのは4次なので、$N=M=4$ の結果を採用するのが望ましいということになります。
今回使用した VB.Net のコードを載せておきます。
Public Shared Sub Lsm_Surface(ByVal Lsm_N As Integer, ByVal Lsm_X() As Single, ByVal Lsm_Y() As Single,
ByVal Lsm_Z() As Single, ByVal Lsm_Deg_N As Integer,
ByVal Lsm_Deg_M As Integer, ByRef Lsm_Coef(,) As Single)
'--------------------------------------------------------------------------
' 最小二乗法による近似曲面の計算
'
' 入力データ
'
' Lsm_N : 入力データ数
' Lsm_X(1~Lsm_N) : Xデータ
' Lsm_Y(1~Lsm_N) : Yデータ
' Lsm_Z(1~Lsm_N) : Zデータ
'
' Lsm_Deg_N : Xの次数
' Lsm_Deg_M : Yの次数
'
' (例)N=2,M=2 のときは、近似曲面は次式となる
'
' Z=a00 +
' a10・x + a01・y + a11・xy +
' a20・x^2 + a02・y^2 + a21・x^2y + a12・xy^2 + a22・x^2y^2
'
' 出力データ
'
' Lsm_Coef(N, M) : 近似曲面の係数
'
' Lsm_Coef(0, 0) : a00
'
' Lsm_Coef(1, 0) : a10
' Lsm_Coef(0, 1) : a01
' Lsm_Coef(1, 1) : a11
'
' Lsm_Coef(2, 0) : a20
' Lsm_Coef(0, 2) : a02
' Lsm_Coef(2, 1) : a21
' Lsm_Coef(1, 2) : a12
' Lsm_Coef(2, 2) : a22
' :
' :
'--------------------------------------------------------------------------
Dim Mtrx_N As Integer, Mtrx_A(,) As Single, ij As Integer, kl As Integer
'行列の大きさ
Mtrx_N = (Lsm_Deg_N + 1) * (Lsm_Deg_M + 1)
ReDim Mtrx_A(Mtrx_N, Mtrx_N + 1)
For i = 1 To Mtrx_N
For j = 1 To Mtrx_N + 1
Mtrx_A(i, j) = 0
Next j
Next i
'行列に変数をセット
For i = 1 To Lsm_Deg_N + 1
For j = 1 To Lsm_Deg_M + 1
ij = (i - 1) * (Lsm_Deg_M + 1) + j '行方向変数
For k = 1 To Lsm_Deg_N + 1
For l = 1 To Lsm_Deg_M + 1
kl = (k - 1) * (Lsm_Deg_M + 1) + l '列方向変数
For m = 1 To Lsm_N '入力点を合計
Mtrx_A(ij, kl) = Mtrx_A(ij, kl) + Lsm_X(m) ^ (i - 1) * Lsm_X(m) ^ (k - 1) *
Lsm_Y(m) ^ (j - 1) * Lsm_Y(m) ^ (l - 1)
If k = Lsm_Deg_N + 1 And l = Lsm_Deg_M + 1 Then
Mtrx_A(ij, kl + 1) = Mtrx_A(ij, kl + 1) + Lsm_Z(m) * Lsm_X(m) ^ (i - 1) *
Lsm_Y(m) ^ (j - 1)
End If
Next m
Next l
Next k
Next j
Next i
Call PGaussJordan(Mtrx_N, Mtrx_A)
For i = 1 To Lsm_Deg_N + 1
For j = 1 To Lsm_Deg_M + 1
ij = (i - 1) * (Lsm_Deg_M + 1) + j
Lsm_Coef(i - 1, j - 1) = Mtrx_A(ij, Mtrx_N + 1)
Next j
Next i
End Sub
Public Shared Sub PGaussJordan(ByVal Mtrx_N As Integer, ByRef AM(,) As Single)
'-----------------------------------------------------------------------------------
' 完全ピボッティングによるガウス・ジョルダン消去法
'-----------------------------------------------------------------------------------
'
' 下記のn元1次連立方程式を解く場合
'
' ┌
' │ a_11・x_1 + a_12・x_2 + ... + a_1n・x_n = b_1
' │ a_21・x_1 + a_22・x_2 + ... + a_2n・x_n = b_2
' │
' │ ......
' │
' │ a_n1・x_1 + a_n2・x_2 + ... + a_nn・x_n = b_n
' └
'
' 入力変数 AM を以下のようにセット
'
' ┌ ┐ ┌ ┐
' │AM(1,1), AM(1,2), ... , AM(1,N), AM(1,N+1)│ │a_11, a_12, ... , a_1n, b_1│
' │AM(2,1), AM(2,2), ... , AM(2,N), AM(2,N+1)│ │a_21, a_22, ... , a_2n, b_2│
' │ │=>│ │
' │ ...... │ │ ...... │
' │ │ │ │
' │AM(N,1), AM(N,2), ... , AM(N,N), AM(N,N+1)│ │a_n1, a_n2, ... , a_nn, b_n│
' └ ┘ └ ┘
'
' 実行後、行列の N+1 列が計算結果になる
'
'
' x_1=AM(1,N+1)
' x_2=AM(2,N+1)
'
' ......
'
' x_n=AM(N,N+1)
'
'-----------------------------------------------------------------------------------
Dim Mtrx_L() As Integer, m As Integer, nm As Integer, Eps As Double
Dim Coef_D As Double, AW As Double, MW As Integer
Dim P As Integer, Q As Integer, KW As Integer, NW As Integer
ReDim Mtrx_L(Mtrx_N)
m = 1
nm = Mtrx_N + m
Eps = 0.000001
For j = 1 To Mtrx_N
Mtrx_L(j) = j
Next j
Coef_D = 1
For k = 1 To Mtrx_N
AW = Math.Abs(AM(k, k))
P = k
Q = k
For j = k To Mtrx_N
For i = k To Mtrx_N
If AW < Math.Abs(AM(i, j)) Then
AW = Math.Abs(AM(i, j))
P = i
Q = j
End If
Next i
Next j
If AW < Eps Then
MessageBox.Show("Error in PGaussJordan (AW=" & Format(AW, "0.00000E+00") & ")",
"Error in PGaussJordan",
MessageBoxButtons.OK, MessageBoxIcon.Exclamation)
Exit Sub
Else
If k <> P Then
Coef_D = -Coef_D
For j = k To nm
AW = AM(k, j)
AM(k, j) = AM(P, j)
AM(P, j) = AW
Next j
End If
If k <> Q Then
Coef_D = -Coef_D
For i = 1 To Mtrx_N
AW = AM(i, k)
AM(i, k) = AM(i, Q)
AM(i, Q) = AW
Next i
MW = Mtrx_L(k)
Mtrx_L(k) = Mtrx_L(Q)
Mtrx_L(Q) = MW
End If
Coef_D *= AM(k, k)
KW = k + 1
For j = KW To nm
AM(k, j) = AM(k, j) / AM(k, k)
Next j
For i = 1 To Mtrx_N
If i <> k Then
For j = KW To nm
AM(i, j) = AM(i, j) - AM(i, k) * AM(k, j)
Next j
End If
Next i
End If
Next k
NW = Mtrx_N + 1
For j = NW To nm
For i = 1 To Mtrx_N
P = Mtrx_L(i)
AM(P, Mtrx_N) = AM(i, j)
Next i
For i = 1 To Mtrx_N
AM(i, j) = AM(i, Mtrx_N)
Next i
Next j
End Sub
連立方程式の解法にはガウス・ジョルダン消去法を使用しています。このアルゴリズムはどのようなケースでも解けるわけではないので、エラーメッセージが表示されたときは適切に対応してください。
最小二乗法による2次元データの近似にどれだけ需要があるのかわかりませんが、ネット上でも情報が少ないようなので紹介しておきます。何かの参考にしてください。