3次元空間での2直線の最接近位置
3D Model を扱う際、2直線の交点を求めたいことがあります。ただし、2次元平面であれば平行でない限り交点は必ずありますが、3次元空間では「ねじれの位置」にあれば交点は存在しません。
このため、交差していない場合は2直線の交点ではなく最接近位置を求め、最接近距離が設定したトレランス以下であれば最接近位置間の中点を交点として代用するという方法が使われることがあります。そこで、2直線の最接近位置を求めるロジックが必要になりますが、これが意外と面倒です。今回はこのロジックについて説明してみます。
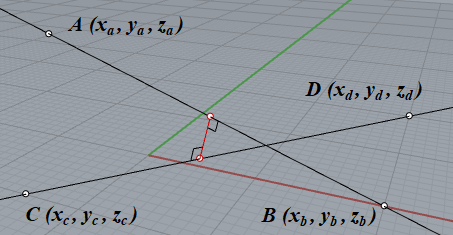
点 $ A(x_a,y_a,z_a), B(x_b,y_b,z_b) $ を通る直線 $ AB $ と点 $ C(x_c,y_c,z_c), D(x_d,y_d,z_d) $ を通る直線 $ CD $ の最接近位置は、2直線のどちらとも垂直に交わる線上にあることになります。
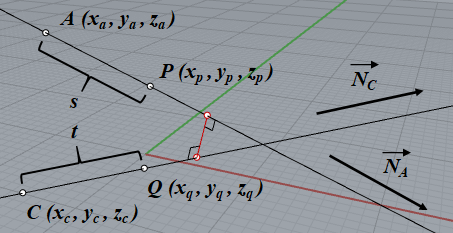
計算方法としては、単位ベクトル $ N_A,N_C $ と媒介変数 $ s,t $ を使用します。単位ベクトルの成分をそれぞれ $ N_A = (N_{Ax}, N_{Ay}, N_{Az}), N_C = (N_{Cx}, N_{Cy}, N_{Cz}) $ とし、下図に示すように直線上の任意の点 $ P(x_p, y_p, z_p), Q(x_q, y_q, z_q) $ を基準点からの距離として表現するわけです。
$$
\begin{eqnarray}
(x_p, y_p, z_p) &=& (x_a + s N_{Ax},\, y_a + s N_{Ay},\, z_a + s N_{Az}) \\
(x_q, y_q, z_q) &=& (x_c + t N_{Cx},\, y_c + t N_{Cy},\, z_c + t N_{Cz})
\end{eqnarray}
$$
$ P,Q $ 間の距離 $ d $ は次式で表されます。平方根を考えると面倒なので距離の2乗で考えます。
$$ d^2 = (x_p – x_q)^2 + (y_p – y_q)^2 + (z_p – z_q)^2 $$
単位ベクトル成分と媒介変数を代入し、途中の展開を省略してまとめると次式になります。
$$
\begin{eqnarray}
f(s,t) &=& d^2 \\
&=& (N_{Ax}^2 + N_{Ay}^2+ Z_{Az}^2)\,s^2 \\
& & +2 \left\{ (x_a – x_c) N_{Ax} + (y_a – y_c) N_{Ay} + (z_a – z_c) N_{Az} \right\}\,s \\
& & -2 (N_{Ax} N_{Cx} + N_{Ay} N_{Cy} + N_{Az} N_{Cz})\,s t \\
& & +2 \left\{ (x_c – x_a) N_{Cx} + (y_c – y_a) N_{Cy} + (z_c – z_a) N_{Cz} \right\}\,t \\
& & + (N_{Cx}^2 + N_{Cy}^2+ Z_{Cz}^2)\,t^2 \\
& & + (x_a – x_c)^2 + (y_a – y_c)^2 + (z_a – z_c)^2
\end{eqnarray}
$$
したがって、この2変数方程式 $ f(s,t) $ が最小になる $s,t$ を求める必要があります。$ f(s,t) $ が最小になるときは変数 $s,t$ に対して勾配がゼロになるので、それぞれで偏微分したときにゼロになるという性質を使用します。
$$
\begin{eqnarray}
\frac{\partial f(s,t)}{\partial s} &=& 2 (N_{Ax}^2 + N_{Ay}^2+ Z_{Az}^2)\,s \\
& & +2 \left\{ (x_a – x_c) N_{Ax} + (y_a – y_c) N_{Ay} + (z_a – z_c) N_{Az} \right\} \\
& & -2 (N_{Ax} N_{Cx} + N_{Ay} N_{Cy} + N_{Az} N_{Cz})\,t \\
&=& 0 \\
\frac{\partial f(s,t)}{\partial t} &=& 2 (N_{Cx}^2 + N_{Cy}^2+ Z_{Cz}^2)\,t \\
& & +2 \left\{ (x_c – x_a) N_{Cx} + (y_c – y_a) N_{Cy} + (z_c – z_a) N_{Cz} \right\} \\
& & -2 (N_{Ax} N_{Cx} + N_{Ay} N_{Cy} + N_{Az} N_{Cz})\,s \\
&=& 0
\end{eqnarray}
$$
この2つの式を連立させて解くことで $ s,t $ が求まり、それによって最接近位置の座標が求まるというわけです。
$$
\begin{eqnarray}
A_1 &=& N_{Ax}^2 + N_{Ay}^2+ Z_{Az}^2 \\
A_2 &=& – (N_{Ax} N_{Cx} + N_{Ay} N_{Cy} + N_{Az} N_{Cz}) \\
A_3 &=& (x_a – x_c) N_{Ax} + (y_a – y_c) N_{Ay} + (z_a – z_c) N_{Az} \\
B_1 &=& – (N_{Ax} N_{Cx} + N_{Ay} N_{Cy} + N_{Az} N_{Cz}) \\
B_2 &=& N_{Cx}^2 + N_{Cy}^2+ Z_{Cz}^2 \\
B_3 &=& (x_c – x_a) N_{Cx} + (y_c – y_a) N_{Cy} + (z_c – z_a) N_{Cz} \\
& & \\
t &=& \frac{A_1 B_3 – A_3 B_1}{A_2 B_1 – A_1 B_2} \\
s &=& – \frac{A_2 t + A_3}{A_1}
\end{eqnarray}
$$
こうやって整理するとわかりやすいのですが、最初にベクトルと媒介変数を使うロジックを考えた人は尊敬します。このあたりが数学的なセンスなんでしょうね。
せっかくなので VB.Net でプログラムを作成してみました。
Public Shared Sub Line_ClosestPoint(ByVal P_XA As Single, ByVal P_YA As Single, ByVal P_ZA As Single,
ByVal P_XB As Single, ByVal P_YB As Single, ByVal P_ZB As Single,
ByVal P_XC As Single, ByVal P_YC As Single, ByVal P_ZC As Single,
ByVal P_XD As Single, ByVal P_YD As Single, ByVal P_ZD As Single,
ByRef P_XP As Single, ByRef P_YP As Single, ByRef P_ZP As Single,
ByRef P_XQ As Single, ByRef P_YQ As Single, ByRef P_ZQ As Single,
ByRef Closest_Dist As Single, ByRef ErrNo As Integer,
Optional ByVal Message_Show As Integer = 0)
'---------------------------------------------------------------------
' ねじれの位置にある空間上の2直線の最接近位置と最接近距離を求める
'
' P_XA~P_ZA, P_XB~P_ZB : 直線(1)上の2点の座標
' P_XC~P_ZC, P_XD~P_ZD : 直線(2)上の2点の座標
'
' P_XP,P_YP,P_ZP : 直線(1)上の最接近位置の座標
' P_XQ,P_YQ,P_ZQ : 直線(2)上の最接近位置の座標
' Closest_Dist : 最接近距離
'
' Message_Show : 1=エラー発生時にメッセージを表示する
'
' ErrNo : 0=エラーなし、1=エラー発生
'---------------------------------------------------------------------
Dim Vector_Ax As Single, Vector_Ay As Single, Vector_Az As Single
Dim Vector_Cx As Single, Vector_Cy As Single, Vector_Cz As Single
Dim Vector_L As Single, Coef_A(3) As Single, Coef_B(3) As Single
Dim Coef_S As Single, Coef_T As Single
ErrNo = 1
P_XP = 0 : P_YP = 0 : P_ZP = 0
P_XQ = 0 : P_YQ = 0 : P_ZQ = 0
Closest_Dist = 0
'直線 A-B の単位ベクトル成分
Vector_Ax = P_XB - P_XA
Vector_Ay = P_YB - P_YA
Vector_Az = P_ZB - P_ZA
Vector_L = Math.Sqrt(Vector_Ax ^ 2 + Vector_Ay ^ 2 + Vector_Az ^ 2)
If Vector_L = 0 Then
If Message_Show = 1 Then
MessageBox.Show("1st line data is invalid. (2 points are same position)",
"Error in Line_ClosestDistance",
MessageBoxButtons.OK, MessageBoxIcon.Exclamation)
End If
Exit Sub
End If
Vector_Ax /= Vector_L
Vector_Ay /= Vector_L
Vector_Az /= Vector_L
'直線 C-D の単位ベクトル成分
Vector_Cx = P_XD - P_XC
Vector_Cy = P_YD - P_YC
Vector_Cz = P_ZD - P_ZC
Vector_L = Math.Sqrt(Vector_Cx ^ 2 + Vector_Cy ^ 2 + Vector_Cz ^ 2)
If Vector_L = 0 Then
If Message_Show = 1 Then
MessageBox.Show("2nd line data is invalid. (2 points are same position)",
"Error in Line_ClosestDistance",
MessageBoxButtons.OK, MessageBoxIcon.Exclamation)
End If
Exit Sub
End If
Vector_Cx /= Vector_L
Vector_Cy /= Vector_L
Vector_Cz /= Vector_L
'連立方程式の係数
Try
Coef_A(1) = Vector_Ax ^ 2 + Vector_Ay ^ 2 + Vector_Az ^ 2
Coef_A(2) = -(Vector_Ax * Vector_Cx + Vector_Ay * Vector_Cy + Vector_Az * Vector_Cz)
Coef_A(3) = Vector_Ax * (P_XA - P_XC) + Vector_Ay * (P_YA - P_YC) + Vector_Az * (P_ZA - P_ZC)
Coef_B(1) = -(Vector_Ax * Vector_Cx + Vector_Ay * Vector_Cy + Vector_Az * Vector_Cz)
Coef_B(2) = Vector_Cx ^ 2 + Vector_Cy ^ 2 + Vector_Cz ^ 2
Coef_B(3) = Vector_Cx * (P_XC - P_XA) + Vector_Cy * (P_YC - P_YA) + Vector_Cz * (P_ZC - P_ZA)
Catch ex As Exception
If Message_Show = 1 Then
MessageBox.Show(ex.Message, "Error in Line_ClosestDistance",
MessageBoxButtons.OK, MessageBoxIcon.Exclamation)
End If
Exit Sub
End Try
'平行判定
If (Coef_A(2) * Coef_B(1) - Coef_A(1) * Coef_B(2)) = 0 Then
If Message_Show = 1 Then
MessageBox.Show("These straight lines are parallel.",
"Error in Line_ClosestDistance",
MessageBoxButtons.OK, MessageBoxIcon.Exclamation)
End If
Exit Sub
End If
'連立方程式の計算
Try
Coef_T = (Coef_A(1) * Coef_B(3) - Coef_A(3) * Coef_B(1)) /
(Coef_A(2) * Coef_B(1) - Coef_A(1) * Coef_B(2))
Coef_S = (-Coef_A(2) * Coef_T - Coef_A(3)) / Coef_A(1)
Catch ex As Exception
If Message_Show = 1 Then
MessageBox.Show(ex.Message, "Error in Line_ClosestDistance",
MessageBoxButtons.OK, MessageBoxIcon.Exclamation)
End If
Exit Sub
End Try
'最接近位置の座標
P_XP = P_XA + Coef_S * Vector_Ax
P_YP = P_YA + Coef_S * Vector_Ay
P_ZP = P_ZA + Coef_S * Vector_Az
P_XQ = P_XC + Coef_T * Vector_Cx
P_YQ = P_YC + Coef_T * Vector_Cy
P_ZQ = P_ZC + Coef_T * Vector_Cz
'最接近距離
Closest_Dist = Math.Sqrt((P_XP - P_XQ) ^ 2 + (P_YP - P_YQ) ^ 2 + (P_ZP - P_ZQ) ^ 2)
ErrNo = 0
End Sub
エラーが発生したときにメッセージボックスを表示するかどうかという引数も加えています。表示したい場合は1に設定してください。
あと、久しぶりに LaTeX でがっつりと数式を書いてみてました。約25年ぶりですが、書いているうちに次第に思い出すものですね。今後も機会があれば数式山盛りでロジックを紹介していくつもりなので、お楽しみに。