3D Model での球の作り方
STL ファイルなど3角形パッチで構成された球の3次元モデルを作成したことがあり、その際の流れについて紹介しておきます。
球の表面を三角形パッチに分割する場合、最初に思いつくのは地球儀のように緯度経度で分割することです。これなら三角関数を駆使するだけで容易に作成できます。

最初はこの手法で作成してみたのですが、これだと球の北極と南極に頂点が集まることになり、高緯度のエリアがものすごく細い三角形で構成されることになります。ちょっと見栄えが悪く、表示だけならまだしも実際に光造形などで実物を作成する際は不具合が起きるかもしれません。

そこで、同じ面積の三角形だけで球が作成できないかと調べたところ、一般的には正20面体を細分化していくという手法が使われるようです。
最初に、球に内接する正20面体を作成します。

各辺の中点を求めます。

球の中心から各辺の中点への直線を作成し、球の表面まで延長して交点を求めます。

その交点を使用して、三角形を4つに分割します。
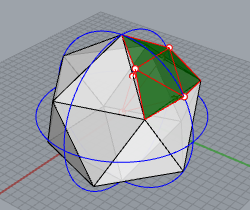
これを繰り返して三角形を細分化していくわけです。プログラムを作成する場合、再帰的なサブルーチンにしておけば十分な精度が得られるまで繰り返すことができます。
試しに細分化を繰り返してみます。
0回(正20面体)

1回

2回

3回

4回

5回

ここまで繰り返せば、画面に表示するのであれば問題ない精度と言えるでしょう。表面を拡大すると、同じ面積の三角形できれいに分割されているのがわかります。

実際に物を作成するのであれば、場合によってはさらに細かくする必要があるかもしれません。ただし、細分化するたびにファイルサイズが4倍ずつ増えてしまうので、その点との兼ね合いになります。
こういうロジックはゲームクリエイターなど普段から3Dポリゴンを扱っている人にとっては常識なんでしょうけど、工学的なエンジニアには知らない人が多いかもしれません(私も調べるまで知りませんでした)。
備忘録として紹介しておきますので、何かの参考にしてください。